Parsing

Today we have a bit of a change of pace: let's come back to the very beginning of our compiler pipeline, the stage between the string input we receive and the AST we send to the compiler and interpreter. We talked early on in the semester about what an AST was and why it was useful to us. There's not much interesting going on in the transformation from the s-expression data type to the expr AST data type. But we left the string-to-s-expression transformation as a black box.

Traditionally, this has been a huge part of compiler design, one of the more theory-heavy parts of the study. We're not going to do it justice with one lecture. We couldn't even do it justice with two weeks. This is just a taste.

Tokenization vs parsing

Our goal is go go from user input (represented as a bare string) to some tree-structured data that our compiler can work with, e.g. our OCaml s_exp type. There are actually two steps in the pipeline here: tokenization and parsing. Tokenization splits the input string into a list of tokens, but being a list, this structure remains flat. The parsing step turns this flat representation into a tree, where the nested nature of the program is clear. What is a token? It could be a parenthesis, or a number, or a symbol.

"(+ 1 (- 3 2))"

----> (tokenizing)

[LPAREN; SYM "+"; LPAREN; SYM "-"; NUM 3; NUM 2; RPAREN; RPAREN]

----> (parsing)

Lst [Sym "+"; Num 1; Lst [Sym "-"; Num 3; Num 2]]

Grammar of s-expressions

Our OCaml S_exp type describes much of how our programs look, but it's not complete. In particular it doesn't have anything to say about parentheses. So let's be a little more precise: we'll write down what's known as a context-free grammar for our programs. (This way of describing grammar is known as Backus-Naur form, and you've seen it at the bottom of each homework handout.)

<s_exp> ::=
| NUM (n)
| SYM (s)
| LPAREN <lst> RPAREN

<lst> ::=
| ε
| <s_exp> <lst>

The symbols that appear in angle brackets, like <s_exp>, are nonterminals. These will not appear in the program string directly, but are useful for expressing our grammar. The other symbols like NUM AND SYM are terminals. Each rule (beginning with |) is called a production rule.

Much like our OCaml data types, we can read these as a list of alternatives: an s_exp is either a number, or a symbol, or a list enclosed in parentheses. But it is also helpful to think of them as enumerating the ways to create an object, hence the name "production rule." For example, suppose we want to create an s_exp. We can pick any rule, say, the third, which says to write an LPAREN, then create a lst, then write an RPAREN. And we see how to create a lst in the following lines.

Here's an example of a larger s-expression created with production rules:

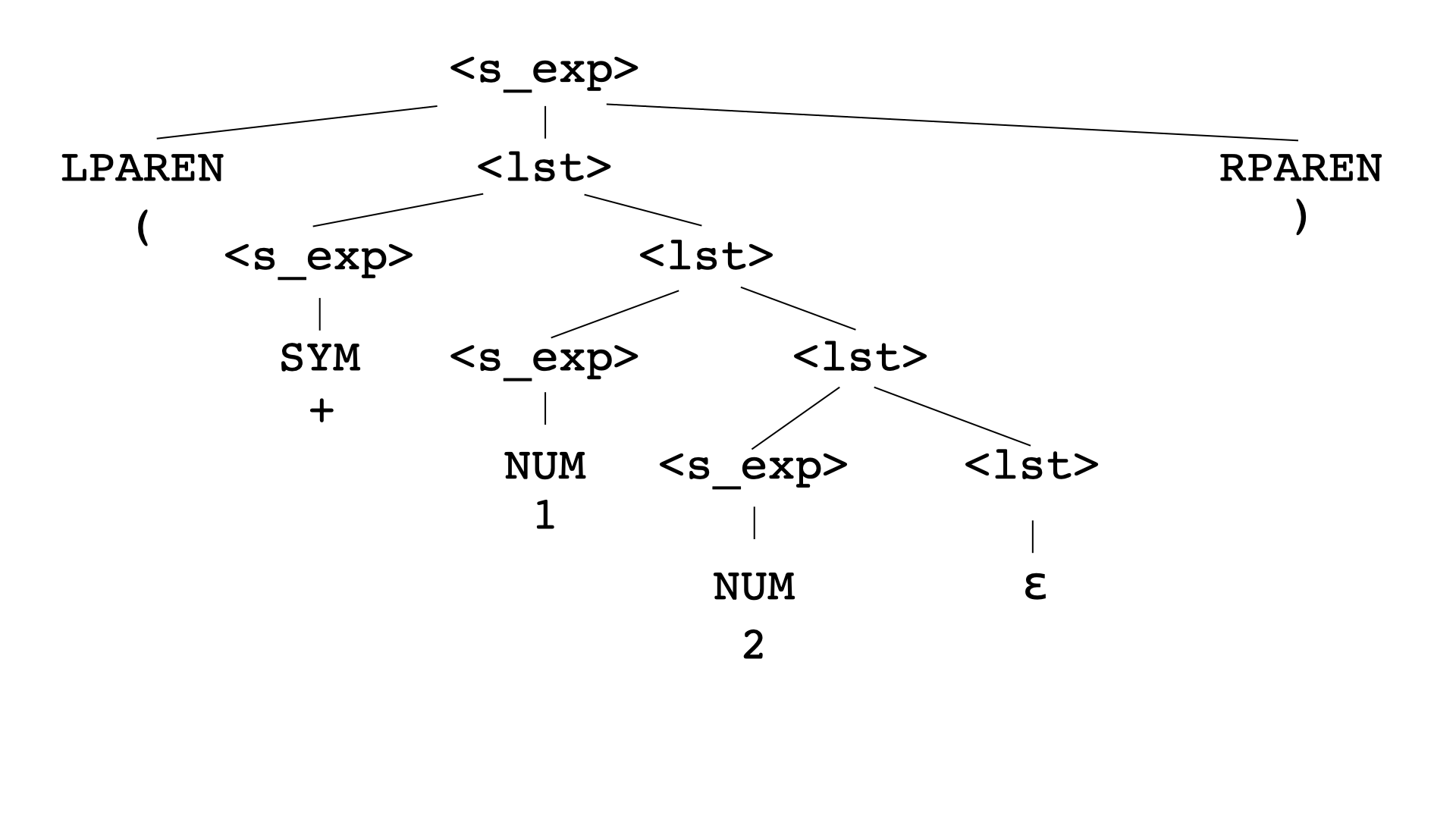
The leaves are all terminals (with associated data), and the internal nodes are all nonterminals. What s-expression does this correspond to?

The "reverse" way to think about this is as a parse tree. Starting with a given string, what does it take to convince ourselves it corresponds to an s-expression? We'd have to show that there's a way of applying a sequence of production rules that creates that string.

Implementing

We're going to start with a very bad tokenizer. Let's not think too hard about it; we'll improve it later.

handparser.ml

type s_exp = Num of int | Sym of string | Lst of s_exp list

type token = NUM of int | SYM of string | LPAREN | RPAREN

exception ParseError

let token_of_string (s : string) =
  match s with
  | "(" ->
      LPAREN
  | ")" ->
      RPAREN
  | _ -> (
    try NUM (int_of_string s) with _ -> SYM s )

let tokenize (s : string) =
  s |> String.split_on_char ' ' |> List.map token_of_string

We'll use a bunch of helper functions to write our parser. These will be chosen in a principled way: each nonterminal in our grammar will have its own parse function, so, parse_s_exp and parse_lst.

Each will consume a list of tokens, and return a list of tokens remaining to be processed. (A parser doesn't need to consume all of its input!) In the case of parse_s_exp, we'll also return an s_exp; in parse_list, we'll also return an s_exp list.

let rec parse_s_exp (toks : token list) : s_exp * token list =
  match toks with
  | NUM n :: toks ->
      (Num n, toks)
  | SYM s :: toks ->
      (Sym s, toks)
  | LPAREN :: toks ->
      let exps, toks = parse_lst toks in
      (Lst exps, toks)
  | _ ->
      raise ParseError

and parse_lst (toks : token list) : s_exp list * token list =
  match toks with
  | RPAREN :: toks ->
      ([], toks)
  | _ ->
      let exp, toks = parse_s_exp toks in
      let exps, toks = parse_lst toks in
      (exp :: exps, toks)

Our grammar has a really nice property: the first token we look at determines which production rule, if any, will match! This means that our helper functions really look very similar to the BNF grammar we wrote above.

One interesting thing to notice is the first case in parse_lst. We wanted to look for the empty string, but how would we look for the empty string, since it’s just ""? Our tokenizer isn’t going to produce that for us. Instead we had to think about what would actually appear next if we had an empty list—which is to say, a right paren! We were able to figure that out by looking at where <lst> is used on the right side of any prouction rules. In this case, <lst> is used exactly once, in the last production rule that has <s_exp> on the left side: <s_exp> ::= LPAREN <lst> RPAREN. In future class sessions, we’ll see how we can use this same approach with other grammars.

For our second <lst> case, things are a bit simpler. We know from the grammar that we expect to see an <s_exp> and then another <lst>. We already have helper functions for parsing those, so we’ll go ahead and call them.

let parse (s : string) =
  let toks = tokenize s in
  let exp, l = parse_s_exp toks in
  if List.length l = 0 then exp else raise ParseError

Tokenizing revisited

The tokenizer we used above was terrible. Traditionally, we don't bulid tokenizers like this. Instead a common approach is to use regular expressions.

Think of a regex as a "string tester." Given a regex and a string, they will either match or not. The grammar of regular expressions is simple and can be written in BNF: (note, this is shorthand and not fully precise)

<regex> ::=
| <string>
| <regex><regex>
| (<regex>|<regex>)
| <regex>*

The first production rule just takes a string literal and matches it literally. For example, the regex abc would match only the string "abc".

The second rule concatenates two regular expressions.

The third rule, as | often does, stands for disjunction. The regex abc|def matches both the strings "abc" and "def".

The fourth ("Kleene star") matches zero or more occurences of the given regex. So a* would match "", "a", "aa", "aaa", ...

For convenience, we'll introduce some shorthand:

X+ := XX*
X? := (X|ε)
(X | Y | Z | ...) := (X | (Y | (Z | ...)))

How could we write a regex that would match numbers?

Maybe something like this:

-?(0|1|2|3|4|5|6|7|8|9)+

And we can continue with this idea. To build a tokenizer for our language, we'll write a regexp (a "recognizer") that matches each token.

NUM := -?(0|1|2|3|4|5|6|7|8|9)+
SYM := (a|b|...|A|B|...|+|-|...)+
LPAREN := (
RPAREN := )

This approach can parse a string of length n in O(n) time.

But: then we need to parse it into a syntax tree. The general problem here -- deciding whether a string of length n is in the language described by an arbitrary context-free grammar -- is not solvable in O(n) time.

There are subsets of context-free grammars that can be parsed in linear time. Broadly speaking, there are two types of these, "top-down" parsers (often written by hand, e.g. LL(k)) and "bottom-up" parsers (often automatically generated, e.g. LR(k), LALR(k)).

Top-down vs bottom-up

We're going to write our parser by hand, so let's focus on the top-down variant. As an upside, it will be flexible and intuitive, and allow for good error messages; as a downside, we may have to adjust our grammar. These parsers generally share some features, some of which we've seen already: we'll use one function per non-terminal in our grammar, and these functions will call each other and themselves ("recursive descent").

The parser we're going to write is an example of an LL(1) parser. The 1 stands for the number of tokens we'll look ahead. Given a list of tokens, we'll want to figure out what production rule to apply; we'll make that decision based only on the first token in the list.

For a grammar that does not have this property, consider a grammar for arithmetic expressions:

<expr> ::=
| NUM
| <expr> + <expr>
| <expr> * <expr>
| (<expr>)

This infix notation is a lot harder to parse than our s-expression language. It's ambiguous! These expressions (and many others) correspond to multiple parse trees:

4 + 5 + 6
1 + 2 * 3

This is inherent to this grammar -- it takes human knowledge to know how we want to parse, say, the second expression here. We could manually resolve it by changing our grammar to something like this:

<expr> ::=
| <term> + <expr>
| <term>

<term> ::=
| <factor> * <term>
| <factor>

<factor> ::=
| NUM 
| (<expr>)

But even though this grammar is now unambigious, it still isn't LL(1). Multiple production rules can start with the same terminal. The predictive parser we wrote before won't handle it.

But! There's yet another trick up our sleeve. The following grammar is equivalent and LL(1):

<expr> ::=
| <term> <expr'>

<expr'> ::= 
| + <expr>
| ε

<term> ::=
| <factor> <term'>

<term'> ::=
| * <term>
| ε

<factor> ::=
| NUM 
| (<expr>)

Let's implement this in OCaml. We actually don't need a helper function for each nonterminal. It's a little cleaner in this case to combine the helper functions for expr and expr'.

handparser2.ml

type token = PLUS | TIMES | LPAREN | RPAREN | NUM of int

type expr = Num of int | Plus of expr * expr | Times of expr * expr

exception ParseError

let rec parse_expr toks =
  let t, toks = parse_term toks in
  match toks with
  | PLUS :: toks ->
      let e, toks = parse_expr toks in
      (Plus (t, e), toks)
  | _ ->
      (t, toks)

and parse_term toks =
  let f, toks = parse_factor toks in
  match toks with
  | TIMES :: toks ->
      let e, toks = parse_term toks in
      (Times (f, e), toks)
  | _ ->
      (f, toks)

and parse_factor toks =
  match toks with
  | NUM n :: toks ->
      (Num n, toks)
  | LPAREN :: toks -> (
      let e, toks = parse_expr toks in
      match toks with RPAREN :: toks -> (e, toks) | _ -> raise ParseError )
  | _ ->
      raise ParseError