IRs and register allocation

The optimizations we've talked about so far have been implemented at the AST level. And indeed, our AST has played a pretty crucial role. Not only does it allow us to ignore irrelevant syntactic details in our compilation step, it even allowed us to support multiple syntaxes for our language.

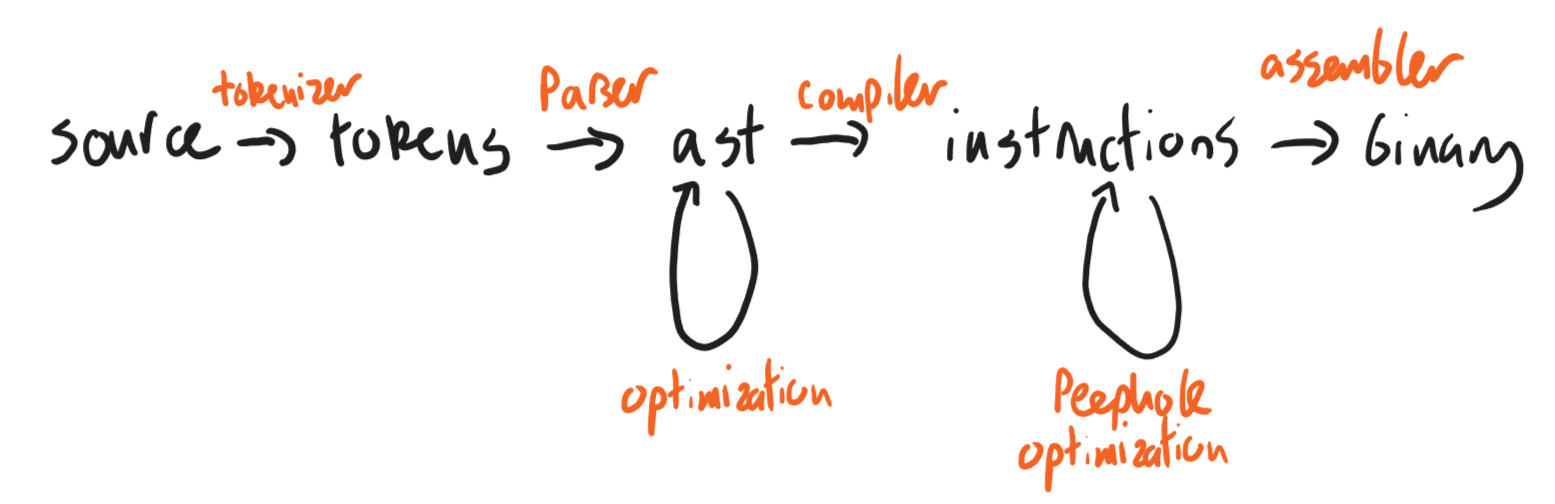
But this was a bit of a white lie. It's not that common to re-use an AST data structure for multiple languages. More often than not, the AST constructors are too tightly coupled to specific language features to make this practical.

Still, we'd like to preserve some of these modular features of the AST. Many compilers do this by adding one more stop in the pipeline, between the AST and assembly stages. This stop is called an intermediate representation (IR) layer, and unlike ASTs, an IR is commonly shared between many languages.

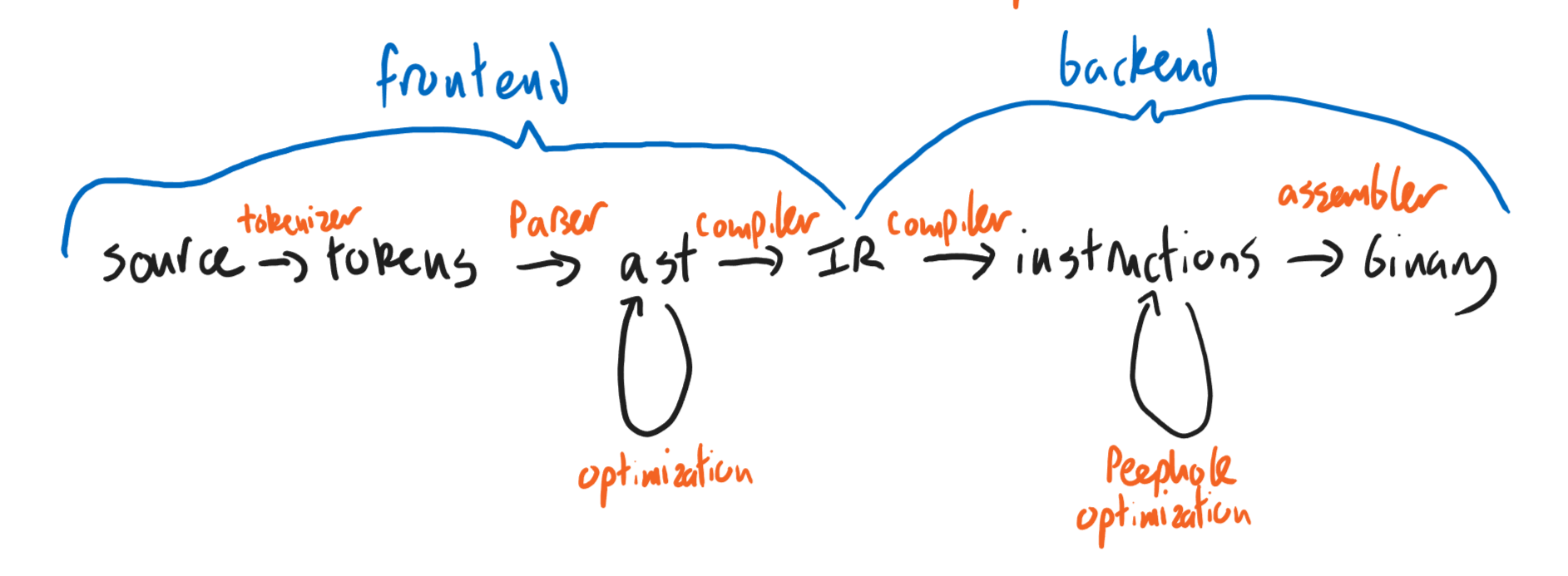
You may have come across the name LLVM in the wild; this is a familiar example of a compiler IR. The gcc C compiler has several internal IRs. Even the OCaml compiler has a few IRs after its AST layer. And a lot of compilers actually use C as an IR, passing on work after that point to a regular C compiler.

Today we're going to describe a prototypical IR, based more or less closely on LLVM. We will describe an optimization most naturally performed at this IR layer.

Basic Blocks

The fundamental components of our IR are called basic blocks. The contents of a basic block look vaguely like assembly directives. A basic block begins with a label and ends with a jump.

Inside a basic block, temporary values (like variables) can be assigned to. The values they are assigned to can be other temporaries, or can be produced by operations on temporaries; the allowed operations generally correspond to basic x86 operations. Critically, the arguments to these operations must be temporaries themselves. Values can also be loaded or stored in memory, with locations given by temporaries.

There is a critical property of basic blocks: each temporary is assigned to exactly once. This property is known as static single assignment (SSA). This property is global: even when we have multiple basic blocks, they cannot reassign each other's variables.

Here's an example of a basic block:

L1:
  t0 <- 2
  t1 <- f(t0)
  t2 <- t0 + t1
  JMP(L2) 

Here's another:

L2:
  t3 <- t2 * t1
  t4 <- LOAD(t1)
  STORE(t1, t3)
  t5 <- t3 <= t2
  CJMP(t5, L3, L4)

It can be illuminating to translate a program in our course language into this style. Since our language doesn't support mutation, preserving SSA is surprisingly straightforward.

(let ((x (+ 2 (* 3 (read-num)))))
  (print (f x)))

L1:
  t0 <- 3 
  t1 <- read_num()
  t2 <- t0 * t1 
  t3 <- 2
  t4 <- t3 + t2
  t5 <- f(t4)
  t6 <- print(t5)

Control flow graphs

Within a basic block, we have no ability to implement conditional behavior. This is managed with jumps between blocks.

(let ((x (if (= 0 (read-num)) 4 5)))
  (print (f x)))

L1: 
  t0 <- 0
  t1 <- read_num()
  t2 <- t1 = t2
  CJMP(t2, L2, L3)

L2:
  t3 <- 4
  JMP(L4)

L3: 
  t4 <- 5
  JMP(L4)

L4:
  t5 <- PHI(L2, t3, L3, t4)
  t6 <- f(t5)
  t7 <- print(t6)

(The PHI operation is a case split on the previous executed block.)

One more bit of terminology:

Given a sequence of blocks like this, we can generate a control flow graph, a directed graph outlining the possible execution paths of our program at the basic block level.

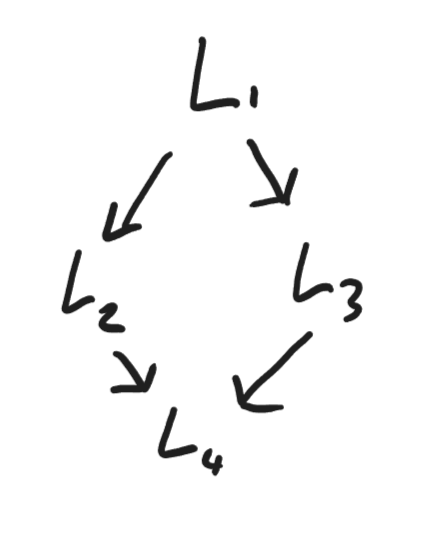
Here are a couple other examples of control flow graphs.

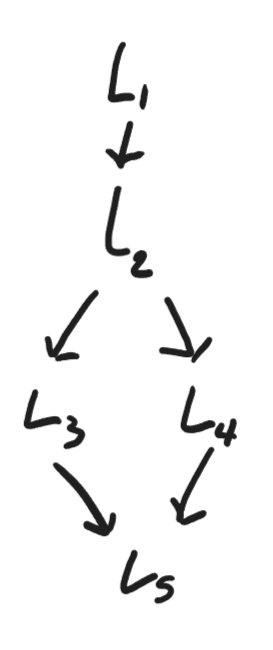
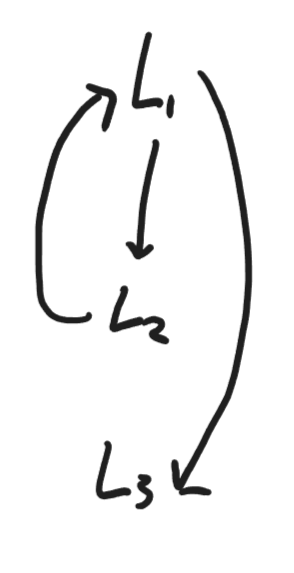
Almost every compiler stores these graphs at some stage. They are essential for implementing a number of important optimizations, including loop optimizations.

One more bit of terminology: a procedure is a control flow graph with entry and exit blocks.

Why is this a useful abstraction? This IR is fairly low level -- it feels similar in many ways to assembly code -- but at the same time, it has abstracted away a lot of the complicated memory management we've had to do. In particular, this language has no reference to the stack! (It does allow heap storage.)

This is interesting, because stack usage versus register usage is something that has kept coming up. A basic block program is agnostic about where values get stored. It has an unlimited number of temporaries, each containing values. Given this high level description, maybe we could use it to identify if and when we can eliminate stack usage in favor of registers.

Register allocation

The stack provides an (approximately) unbounded number of storage locations. Registers don't: the exact number depends on our architecture, but we have, say, 16 available. Nonetheless, many programs don't need to store 16 values at any given time, and we could optimize their performance by using registers instead of stack space.

Register allocation (easy to view as an optimization pass) is a process that will look at a basic block and identify how many memory locations will be needed to execute it. The process analyzes each line of a basic block to determine which temporaries are "live" at the end of that line, that is, which temporaries will affect later lines. This analysis shows us the "life span" of any given temporary, as well as how many temporaries are alive at any given time.

L1:
  t0 <- 4          : 
  t1 <- read_num() : t0
  t2 <- t0 + t1    : t0, t1
  t3 <- t2 * t1    : t1, t2
  t4 <- read_num() : t2, t3
  t5 <- t4 - t3    : t2, t3, t4
  t6 <- t2 + t5    : t2, t5
                   : t6

No temporaries that are simultaneously alive can be stored in the same location. So we want to find a set of locations for these temporaries that will avoid conflicts.

We construct an interference graph: its nodes are temporaries and an edge between two temporaries indicates a conflict (i.e. that they are simultaneously alive).

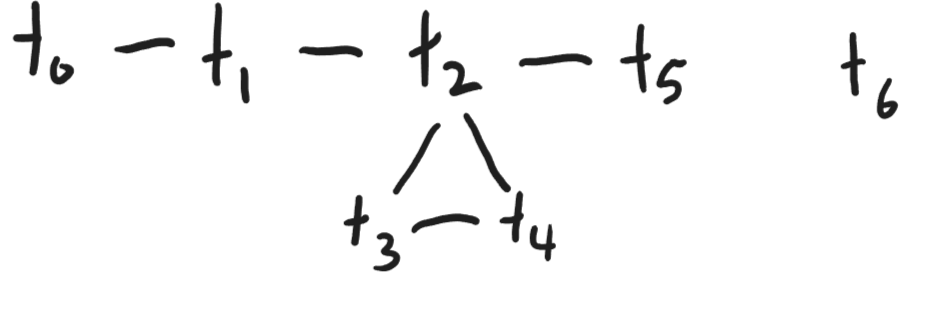
Now a familiar friend pops up out of nowhere: let's represent locations by colors. Then this problem is exactly a graph coloring problem!

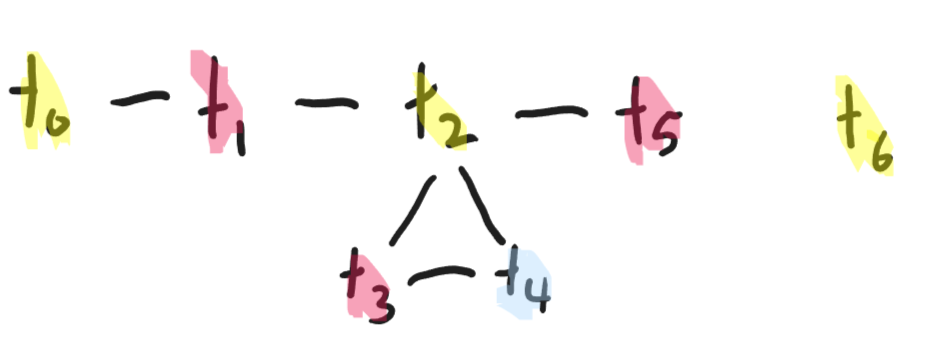
So, given any procedure, we can determine how many memory locations we'll need, and allocate locations to particular values. We won't always be able to do this with registers alone, forcing us to spill over into the stack. But there is potential for significant speedup here. And this is the kind of optimization that is nearly impossible to do at the AST level -- it's inherently too close to the machine-level implementation.